|
TEST
100 years ago: Sewell Wright's inbreeding coefficient
The negative effects of inbreeding had already been described by
Darwin in the 19th century. However, he, and animal breeders, were
aware that uniformity of offspring and anchoring of positive traits
in a breed is not possible without kinship breeding. With smaller
populations, as in pigeon breeding, the mating of closer relatives,
inbreeding, occurs automatically. The question of potential negative
effects in highly inbred strains was tackled by Sewell Wright in the
1920s. He sought a balance between the positive effects of
purebredness (uniformity of offspring and heritability of positive
traits) and the negative ones (vitality and fertility).
Uniformity of offspring in constituent traits of breeds such as
size, feather structures, behaviour
For many traits homozygosity is desirable and from experience not
negative for vital functions. Those who breed plain-headed pigeons
are not happy when a youngster with a feather crest occasionally
lies in the nest due to heterozygosity for the crest. Where a medium
body size is aimed at, oversize and undersize are disturbing in the
offspring. The goal is pure heredity for the expression of a trait
as defined in the standard. From this point of view, mating with
other strains is associated with the risk of losing a strain that
has been painstakingly achieved in terms of pure heredity.
Uncovering of negative traits in the strain through kinship breeding
Inbreeding also reveals recessive vitality-reducing and, in extreme
cases, lethal factors in a strain. From this point of view, web-foot
up to lethal web-lethal, polydactyly and others are the negative
face of inbreeding. But it is not only negative that they show
themselves. This is because consistent breeders have the opportunity
to determine carriers and potential carriers and to eliminate the
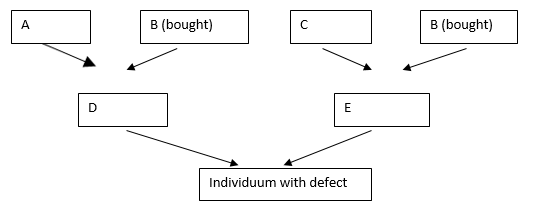
trait in the strain. D and E are latent carriers in the example due
to their descent from B. The siblings of D and E are also highly
likely carriers, as are the siblings of the affected homozygous
individual.
Outwardly imperceptible traits
With advances in molecular genetics, one can look deeper into the
genome than with the naked eye. For example, different alleles in
the feather keratin gene and also in the LDH gene, which plays a
role in the conversion of lactic acid (lactate), can be detected
(cf. the overview article by Eberhard Haase 2021). While studies in
racing pigeons showed that even top flyers do not necessarily have
to be homozygous for the same alleles, earlier studies on
transferrin genotypes, which play a role in the transport of iron
produced in the liver, showed that homozygosity for certain alleles
can have a negative influence on vital functions. In the case of
permanent inbreeding, negative constellations can also accumulate in
families for other genes that have not been studied so far and thus
trigger what is called inbreeding depression.
The calculation of the inbreeding coefficient
The inbreeding coefficient developed by Wright calculates the
potential inbreeding degree of an animal from a pedigree, as shown
in the example. Potential, because it determines the probability
that two genes of a gene locus are of the same parentage. The same
or identical parentage means that they come from the same ancestor
and have been passed down through the generations.
In the example, it is ancestor B who is common on both the maternal
and paternal sides through parents D and E. According to Wright, if
A, B, C have no common ancestors to be considered, then the
coefficient Fj for the individual j is
Fj = Σ (1/2)n1+n2+1, where n1 is the number of
generations from parent D to common ancestor B (here = 1) and n2 is
the number of generations from E to common ancestor B (here also =
1). The summation sign Σ refers to the fact that there can be
several common ancestors. A value is then calculated for each
ancestor and then added together. For the half-sibling pairing
shown, an inbreeding coefficient of
Fj = (1/2)3 = 0.125.
For the mating of full siblings, the value will double, 0.250.
The parallels to inheritance processes
The formula for the coefficient may look like magic at first glance.
But it has as its background the same genetic understanding that is
also expressed in Mendel's laws and in the representation of
Punnett's squares. Let us assume that full siblings are mated with
each other whose parents are genetically unrelated. On a locus in
the genome, let one parent have alleles 1 and 2 and the other
alleles 3 and 4. With a large number of offspring, four gene
combinations could fall out of this, (1//3), (1//4) and (2//3) as
well as (2//4). With a very large number of random full sibling
matings, 1/16 of the young in the subsequent generation are
homozygous for allele 1. In the statistical expectation, 1/16 of the
young are also homozygous for each of the other three alleles,
making a total of 4/16 or ¼ or the 0.250 given in Wright's formula.
Almost more significant for the above discussion of inbreeding
depression: the probability that a young of F2 does not
have a gene, e.g. gene 1, is one quarter. If by chance two such
young animals are mated with each other for further breeding the
next generation, then allele 1 has disappeared in the inbred line.
The probability of such a coincidence is statistically ¼ x ¼ = 1/16.
This seems small, but it also applies to the definitive loss of one
of the other alleles and to other genes of the entire genome. There
is an increase in pure heredity over the generations and, as the
other side of the coin, a loss of alleles in the family. With the
transferrin genotypes, traits have been found where this can be
harmful. This will only be the tip of the iceberg.
On the usefulness of the inbreeding coefficients
The calculations are not comparable to the molecular genetic
analysis of individuals, ancestries and similarities within
populations. These were not possible in Wright's time and are hardly
possible for pigeon fanciers today. What remains is the coefficient
as an easier point of reference to determine. The absolute numbers
are not so important in themselves, the differences in different
breeding strategies perhaps even more so. At least they show the
beginner that it is better to start breeding with two pairs than
with one pair. The measured inbreeding coefficient when siblings of
the offspring from unrelated parents are mated with each other is
calculated as 0.250, when siblings are mated again it rises to
0.375. If offspring of another unrelated pair are available for
cross breeding, the measured coefficient of the offspring of the
first generation drops to zero, when cross breeding it rises to a
more moderate 0.125 in the second generation and opens up the
possibility of less close relationship breeding for some time. For a
more detailed analysis see Sell 2012, 2019. (AS)
Literature:
Haase, Eberhard, Molekulargenetik und Brieftaubenzucht, Die
Brieftaube no. 25, June 26, 2021, pp. 6-10.
Sell, Critical Issues in Pigeon Breeding. What we know and what we
believe to know, Part VI, Achim 2021
Sell, Pigeon Genetics. Applied Genetics in the Domestic Pigeon,
Achim 2012
Sell, Taubenzucht. Möglichkeiten und Grenzen züchterischer
Gestaltung, Achim 2019.
Wright, Sewall, Coefficients of Inbreeding and Relationships, The
American Naturalist Vol. 56, No. 645 (Jul. - Aug., 1922), pp.
330-338.

Homozygous family of Thuringian White-Bib Pigeon in respect to
constitutional characteristics of the breed
 
Defective web-feet in a family that from time to time shows up in
inbred families. As is shown, the webs also lead to a curvature of
the toe position.
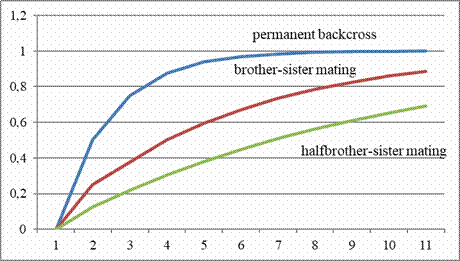
Inbreeding Coefficients of Wright in different inbreeding
strategies.
Source: Sell, Taubenzucht. Möglichkeiten und Grenzen züchterischer
Gestaltung. Zucht und Vererbung in Theorie und Praxis, Achim 2019

Youngsters in the same age with different inbreeding coefficient due
to cross-fertilization (young in the background). Source: Sell,
Taubenzucht, Achim 2019.
|